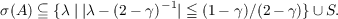|
Given a regular matrix A,
Mercerian theorems are concerned with determining the real or complex values of α
for which αI + (1 − α)A is equivalent to convergence. For α≠1, the problem is
equivalent to determining the resolvent set for A, or, determining the spectrum
σ(A) of A. where σ(A) = {λ∣A − λI is not invertible}. This paper treats
the problem of determining the spectra of weighted mean methods; i.e.,
triangular matrices A = (ank) with an k = pk∕Pn, where p0 > 0, pn ≧ 0,
∑
k=0npk = Pn. It is shown that the spectrum of every weighted mean method is
contained in the disc {λ∣|λ − 1∕2|≦ 1∕2} (Theorem 1), and, if limpn∕Pn
exists,
| σ(A) | = {λ∣|λ − (2 − 𝜖)−1|≦ (1 − 𝜖)∕(2 − 𝜖)} | |
| | ∪{pn∕Pn∣pn∕Pn < 𝜖∕(2 − 𝜖)}, | | |
where 𝜖 = limpn∕Pn.
Let γ = 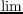 pn∕Pn, δ = pn∕Pn, δ = 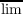 pn∕Pn, S = {pn∕Pn∣n ≧ 0}. When γ < δ, some
examples are provided to indicate the difficulty of determining the spectrum
explicitly. It is shown that {λ∣|λ − (2 − δ)−1|≦ (1 − δ∕(2 − δ))}∪ S ⊆ σ(A)
and pn∕Pn, S = {pn∕Pn∣n ≧ 0}. When γ < δ, some
examples are provided to indicate the difficulty of determining the spectrum
explicitly. It is shown that {λ∣|λ − (2 − δ)−1|≦ (1 − δ∕(2 − δ))}∪ S ⊆ σ(A)
and
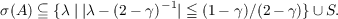
Theorem 1 is a generalization of the corresponding theorems of: S. Aljancic, L. N.
Cakalov, K. Knopp, M. E. Landau, J. Mercer, Y. Okada, W. Sierpinski, and G.
Sunouchi.
|