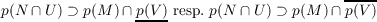|
Let K be a closed subspace in a
real or complex normed linear space L. The “Main Interpolation Problem” as
formulated by L. Asimow reads as follows: Given a bounded convex neighborhood V
of 0 in L and a bounded closed convex U containing 0, their polars V 0 and U0 in
the dual L′ of L, define the functionals on LpV K(x) = sup(x,V 0 ∩ K0)
and pU(x) = sup(x,U0). For x0 ∈ L we are looking for an element x ∈ L
satisfying
- x − x0 ∈ K(x|K0 = x0|K0) and
- pU(x) = pV K(x0) (exact solution), respectively
- pU(x) ≦ pV K(x0) + 𝜖 for given 𝜖 > 0 (approximate solution).
The problem is formulated in a different but equivalent way in this paper using the
canonical projection p from L to L∕K. For a real linear subspace M of L, a convex
cone N in M and bounded closed convex neighborhoods U and V we prove
conditions in terms of the dual space of L which are necessary and sufficient for the
inclusions
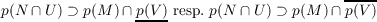
({⋯} means the topological interior, {⋯}, the closure).
|