|

|

|
|
The boundedness of the
Cantor-Bendixson order of some analytic sets
R. Daniel Mauldin |
|
Vol. 74 (1978), No. 1, 167–177
|
Abstract |
|
Let X and Y be complete separable metric spaces (Polish spaces). If E is a subset of X × Y , and x ∈ X, then by the x-section of E, Ex, is meant E ∩ ({x}× Y ). By Ps(E) is 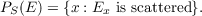 In this paper the following uniform boundedness principle for the Cantor-Bendixson order of analytic sets will be demonstrated. Theorem L. Let W be an analytic subset of X × Y and let M be an analytic subset of X such that M ⊂ PS(W). Then there is a countable ordinal α such that the α-th Cantor-Bendixson derived set of Ex is empty, for each x in M. |
Mathematical Subject Classification 2000
Primary: 54H05
|
Milestones
Received: 15 March 1976
Published: 1 January 1978
|
Authors |
| R. Daniel Mauldin | |
| Department of Mathematics University of North Texas Denton TX 76203-1430 United States |
|
| www.math.unt.edu/~mauldin | |
 |
