Transcendental constants over the coefficient fields in differential elliptic function fields

Keiji Nishioka

Vol. 74 (1978), No. 1, 191–197

DOI: 10.2140/pjm.1978.74.191

Abstract

Let k be a differential field of characteristic 0, and Ω be a universal extension of k. Suppose that the field of constants k₀ of k is algebraically closed. Consider the following dlfferential polynomial of the first order over k in a single indeterminate y: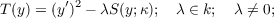

here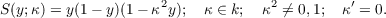

Take a generic point z of the general solution of T. Then, z is transcendental over k, and k(z,z′) is called a differential elliptic function field.

We prove the following:

Theorem. Let k(z,z′) be a differential elliptic function field over k. Then, there exists a finitely generated differential extension field k^∗ of k such that the following three conditions are satisfied:

1. z is transcendental over k^∗;
2. the field of constants of k^∗ is the same as k₀;
3. there exists an element ζ of Ω such that k^∗(z,z′) = k^∗(ζ,ζ′) and (ζ′)² = 4S(ζ;κ) with the same modulus as κ.

Mathematical Subject Classification 2000

Primary: 12H05

Secondary: 34A20

Milestones

Received: 24 November 1976

Revised: 20 July 1977

Published: 1 January 1978