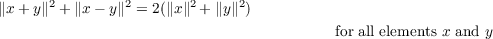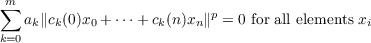Banach spaces which satisfy linear identities

Bruce Reznick

Vol. 74 (1978), No. 1, 221–233

DOI: 10.2140/pjm.1978.74.221

Abstract

In 1935, Jordan and von Neumann proved that any Banach space which satisfies the parallelogram law

(1)

must be a Hilbert space.

Subsequent authors have found norm conditions weaker than (1) which require a Banach space to be a Hilbert space. Notable examples include the results of Day, Lorch, Senechalle and Carlsson.

In this paper, we study nontrivial linear identities such as

(2)

on a Banach space X.

Mathematical Subject Classification 2000

Primary: 46B99

Milestones

Received: 5 May 1977

Revised: 27 July 1977

Published: 1 January 1978