An inequality involving the length, curvature, and torsions of a curve in Euclidean n-space

Joel Larry Weiner

Vol. 74 (1978), No. 2, 531–534

DOI: 10.2140/pjm.1978.74.531

Abstract

Let x be a closed nondegenerate Cⁿ curve in Eⁿ parametrized by arc length s. We prove an inequality for such x which lie in a ball of radius R. For nonplanar curves in E³ the inequality is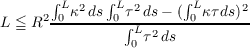

where L is the length of x, and κ and τ are the curvature and torsion of x, respectively. Equality holds only if x is a great circle on a sphere of radius R. We also obtain from the general inequality necessary conditions on the length, curvature, and torsions of x in order that x be a closed curve or a closed curve with at most one corner.

Mathematical Subject Classification 2000

Primary: 53A05

Milestones

Received: 11 July 1977

Published: 1 February 1978