Conjugate points for nonlinear differential equations

Kurt Kreith and Charles Andrew Swanson

Vol. 75 (1978), No. 1, 171–184

DOI: 10.2140/pjm.1978.75.171

Abstract

Much of the classical Sturm oscillation theory has a natural generalization to linear selfadjoint differential equations of order 2n if the notion of successive zeros is replaced by that of n − n conjugate points. Specifically, the smallest β > α such that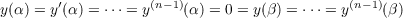

is satisfied by a nontrivial solution of the equation is called the first conjugate point of α and denoted by η₁(α).

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 9 June 1976

Published: 1 March 1978