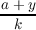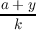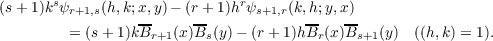|
|
Abstract
|
|
Radamacher has defined a
generalized Dedekind sum
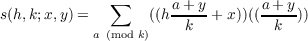
and proved a reciprocity theorem for this sum that generalizes the well known result
for s(h,k). In the present paper we define
| ϕr,s(h,k;x,y) | = ∑
a (mod k)Br(h(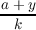 ) + x)Bs( ) + x)Bs(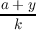 ), ), | |
| | ψr.s(h,k;x,y) | = ∑
j=0r(−1)r−j hr−jϕ
j,r+s−j(h,k;x,y), hr−jϕ
j,r+s−j(h,k;x,y), | | |
where Bn(x) is the Bernoulli function, and show that
We also prove the polynomial reciprocity theorem
![k∑−1 h−[(ha+z)∕k] a h∑−1 k−[(kb+z)∕h] b h k
(1− v) u v − (1− u) v u = u − v ((h,k ) = 1)
a=0 b=0](a055x.png)
as well as some related results.
|
Mathematical Subject Classification
Primary: 10A20, 10A20
Secondary: 10A15
|
Milestones
Received: 13 September 1976
Published: 1 April 1978
|
|
|
|
|


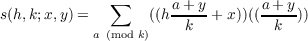
![k∑−1 h−[(ha+z)∕k] a h∑−1 k−[(kb+z)∕h] b h k
(1− v) u v − (1− u) v u = u − v ((h,k ) = 1)
a=0 b=0](a055x.png)