Potential operators and equimeasurability

Ata Nuri Al-Hussaini

Vol. 76 (1978), No. 1, 1–7

DOI: 10.2140/pjm.1978.76.1

Abstract

W. Rudin proved the following.

Theorem 1.1. Assume 0 < p < ∞, p≠2,4,6,⋯ . Let n be a positive integer. If f_i ∈ L_p(μ), g_i ∈ L_p(ν) for 1 ≦ i ≦ n and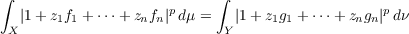

for all (z₁,⋯,z_n) ∈ Cⁿ, then (f₁,⋯,f_n) and (g₁,⋯,g_n) are equimeasurable. Here as usual L_p(μ) and L_p(ν) stand for p-th power integrable functions defined on finite measure spaces (X,X,μ) and (Y,Y,ν) respectively. 𝒞 is the field of complex numbers.

The purpose of this paper is to provide a new setting for Rudin’s result by recasting it and its extension to real valued functions into the framework of the theory of potential operators as formulated by K. Yosida.

Mathematical Subject Classification 2000

Primary: 60J45

Secondary: 46E30

Milestones

Received: 20 May 1977

Published: 1 May 1978