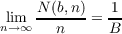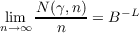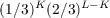|
Let x be a real number,
0 ≦ x < 1, and let 0.x1x2⋯ be its expansion in the base B. Let N(b,n) be the number
of occurrences of the digit b in x up to xn. Then x is called digit normal (in the base
B) if
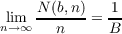
for each of the B possible values of b. Let γ be any fixed B-ary sequence of length L
and N(γ,n) be the number of indices k for which xkxk+1⋯xk+L−1 is γ, that is,
N(γ,n) is the number of times γ appears in the first n digits of x. Then x is normal
(in the base B) if
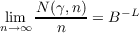
for each of the BL possible sequences γ, and B−L is called the limiting frequency of
γ in x.
The purpose of this paper is to construct a generalized normal number (in the
base 2) in which these frequencies are weighted. For example, we will obtain infinite
binary decimals in which the limiting frequency of occurrence of ones is 1/3 (in
general, p < 1) rather than 1/2; consequently, any binary string γ of length L will
have limiting frequency
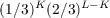
where K is the number of ones in γ.
|