On the metric theory of Diophantine approximation

Jeffrey D. Vaaler

Vol. 76 (1978), No. 2, 527–539

DOI: 10.2140/pjm.1978.76.527

Abstract

A conjecture of Duffin and Schaeffer states that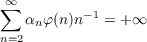

is a necessary and sufficient condition that for almost all real x there are infinitely many positive integers n which satisfy |x − a∕n| < α_nn⁻¹ with (a,n) = 1. The necessity of the condition is well known. We prove that the condition is also sufficient if α_n = O(n⁻¹).

Mathematical Subject Classification

Primary: 10K10, 10K10

Milestones

Received: 29 April 1977

Published: 1 June 1978