The number of nonfree components in the decomposition of symmetric powers in characteristic p

Gert Einar Torsten Almkvist

Vol. 77 (1978), No. 2, 293–301

DOI: 10.2140/pjm.1978.77.293

Abstract

If G is the group with p (=prime) elements and k a field of characteristic p let V ₁,V ₂,⋯,V _p denote the indecomposable k[G]-modules of k-dimension 1,2,⋯,p respectively. Let e_n,ν denote the number of nonfree components of the decomposition of the symmetric power S^νV _n+1. Then the following symmetry relation is proved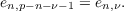

As a corollary we find that S^rV _n+1 has exactly one nonfree component when n + r = p − 2 thus solving a problem in a previous paper by R. Fossum and the author. An explicit formula for e_n,ν expressed in numbers of restricted partitions is obtained.

Mathematical Subject Classification 2000

Primary: 13F20

Secondary: 14C99, 15A72

Milestones

Received: 22 September 1977

Published: 1 August 1978