|

|

|
|
Central moments for
arithmetic functions
Joseph Eugene Collison |
|
Vol. 77 (1978), No. 2, 307–314
|
Abstract |
|
The only central moment considered in probabilistic number theory up until now has been the “variance” of an arithmetic function. This paper considers the case of higher central moments for such functions. It will be shown that if f is an additive complex valued arithmetic function then 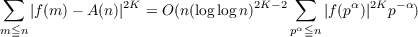 where K is a positive integer and 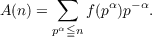 It will also be shown that if f is an additive real valued arithmetic function and K is an odd positive integer, then 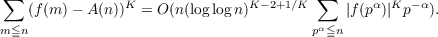 |
Mathematical Subject Classification
Primary: 10K20, 10K20
|
Milestones
Received: 19 May 1977
Published: 1 August 1978
|
Authors |
| Joseph Eugene Collison | |
 |
