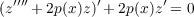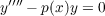On the oscillatory and asymptotic behavior of solutions of fifth order selfadjoint differential equations

Willie Taylor

Vol. 77 (1978), No. 2, 557–563

DOI: 10.2140/pjm.1978.77.557

Abstract

In this paper the fifth order selfadjoint differential equation

(1)

is considered under the assumption that p(x) is a positive continuous function defined on the half axis [0,∞). The oscillation and asymptotic properties of certain solutions of (1) will be discussed after which connections between the solutions of (1) and the solutions of the fourth order differential equation

(2)

are investigated. More spcifically, it is shown that (1) is oscillatory if and only if (2) is oscillatory.

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 3 October 1977

Published: 1 August 1978