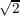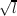The 2-class group of biquadratic fields. II

Ezra Brown and Charles John Parry

Vol. 78 (1978), No. 1, 11–26

DOI: 10.2140/pjm.1978.78.11

Abstract

We describe methods for determining the exact power of 2 dividing the class number of certain cyclic biquadratic number fields. In a recent article, we developed a relative genus theory for cyclic biquadratic fields whose quadratic subfields have odd class number; we considered the case in which the quadratic subfield is Q() with l ≡ 5 (mod 8) a prime. Here we shall extend our methods to the cases in which the subfield is Q() or Q() with l ≡ 1 (mod 8) a prime. We consider all such cases for which the 2-class group of the biquadratic field is of rank at most 3.

Mathematical Subject Classification

Primary: 12A30, 12A30

Milestones

Received: 23 February 1977

Published: 1 September 1978