On relations for representations of finite groups

Christopher Lloyd Morgan

Vol. 78 (1978), No. 1, 157–159

DOI: 10.2140/pjm.1978.78.157

Abstract

Let G be a finite group, and suppose that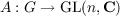

is a (complex) representation of G with character χ. A (complex) linear relation for A is a formal complex linear combination ∑ _g∈Ga_gg such that ∑ _g∈Ga_gA(g) = 0.

We prove the following theorem, which determines the linear relations in terms of the character χ.

Theorem. Let A be a representation for a finite group G, let χ be the character of A, and let {g₁,⋯,g_k} be a subset of G. Then ∑ _j=1^ka_jg_j is a relation for A if and only if ∑ _j=1^kχ(g_ig_j⁻¹)a_j = 0, for all i = 1,⋯,k.

Mathematical Subject Classification 2000

Primary: 20C15

Milestones

Received: 30 June 1977

Revised: 21 January 1978

Published: 1 September 1978