A spectral sequence for the homology of an infinite delooping

Haynes Miller

Vol. 79 (1978), No. 1, 139–155

DOI: 10.2140/pjm.1978.79.139

Abstract

Let E = {E_n : n ∈ Z} be a (−1)-connected infinite loop space: i.e., ΩE_n+1 = E_n for all n, and for n ≧ 0 the space E_n is (n − 1)-connected. Then the stable homology of E is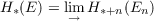

under the suspension homomorphisms. One also has the unstable homology H_∗(E₀), which with mod p coefficients carries a Pontrjagin product and an action of the mod p Dyer-Lashof algebra R.

It is natural to ask how H_∗(E₀) determines H_∗(E); and the purpose of this paper is to construct and study the general properties of a spectral sequence whose E²-term depends functorially on H_∗(E₀) as an R-Hopf algebra and whose E^∞-term is the associated graded module of a natural filtration on H_∗(E). For simplicity we mainly treat the case p = 2.

Mathematical Subject Classification 2000

Primary: 55P47

Secondary: 55S12, 55T99

Milestones

Received: 24 October 1977

Published: 1 November 1978