Solution for an integral equation with continuous interval functions

John Albert Chatfield

Vol. 80 (1979), No. 1, 47–57

DOI: 10.2140/pjm.1979.80.47

Abstract

Suppose R is the set of real numbers and all integrals are of the subdivision-refinement type. Suppose each of G and H is a function from R ×R to R and each of f and h is a function from R to R such that f(a) = h(a), dh is of bounded variation on [a,x], and ∫ _a^xH² = ∫ _a^xG² = 0 for x > a. The following two statements are equivalent:

(1) If x > a, then f is bounded on [a,x], ∫ _a^xH exists, ∫ _a^xG exists, (RL)∫ _a^x(fG + fH) exists, and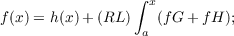

(2) If a ≦ p < q ≦ x, then each of ⋅_p Π^q(1 + H) and ⋅_p Π^q(1 − G)⁻¹ exists and neither is zero,

exists, and

f(x)	= f(a)⋅a Πx(1 + H)(1 − G)−1
	+ (R)∫ ax[⋅ t Πx(1 + H)(1 + G)][(1 − G)−1]dh.

Mathematical Subject Classification 2000

Primary: 45N05

Secondary: 26A42, 44A40

Milestones

Received: 16 July 1976

Published: 1 January 1979