|

|

|
|
Dedekind’s problem:
monotone Boolean functions on the lattice of divisors of an
integer
Paul Hess |
|
Vol. 81 (1979), No. 2, 411–415
|
Abstract |
|
This paper is concerned with the combinatorial problem of counting the number of distinct collections of divisors of an integer N having the property that no divisor in a collection is a multiple of any other. It is shown that if N factors into primes N = p1a1p2a2⋯pnan the number of distinct collections of divisors with the stated property does not exceed (∑ i=1nai −n + 3)M, where M is the maximum coefficient in the expansion of the polynomial 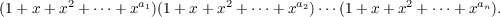 |
Mathematical Subject Classification 2000
Primary: 06B99
Secondary: 05A15
|
Milestones
Received: 6 April 1978
Revised: 14 September 1978
Published: 1 April 1979
|
Authors |
| Paul Hess | |
 |
