Approximation and harmonic continuation of axially symmetric potentials in E³

Peter A. McCoy

Vol. 81 (1979), No. 2, 481–491

DOI: 10.2140/pjm.1979.81.481

Abstract

Let F = F(x,y) be a complex valued axisymmetric potential (ASP) regular in the closed unit sphere about the origin in E³. Let the error in the approximation of F over ℛ_n,ν (where ℛ_n,ν is the set of all Newtonian potentials R_n.ν ≡ P_n^∗(1∕Q_ν) generated from axisymmetric harmonic polynomials P_n and Q_ν by quasimultiplication) be defined by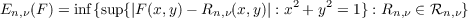

n,ν = 0,1,2,⋯ . Then properties of the sequence {ρ_ν}_ν=0^∞, ρ_ν⁻¹ = limsup_n→∞[E_n,ν(F)]^1∕n, determine:

(i) the sphere to which F continues as an ASP with atmost (precisely) ν-singular circles (ii) the largest sphere of continuation as an ASP and (iii) the NASC for a sphere to contain infinitely many singular circles of the continuation of F.

Mathematical Subject Classification 2000

Primary: 31B15

Milestones

Received: 31 May 1978

Published: 1 April 1979