|

|

|
|
On a theorem of
Murasugi
Cameron Gordon and Richard A. Litherland |
|
Vol. 82 (1979), No. 1, 69–74
|
Abstract |
|
1. Let l = k1 ∪ k2 be a 2-component link in S3, with k2 unknotted. The 2-fold cover of S3 branched over k2 is again S3; let k1(2) be the inverse image of k1, and suppose that k1(2) is connected. How are the signatures σ(k1), σ(k1(2)) of the knots k1 and k1(2) related? This question was considered (from a slightly different point of view) by Murasugi, who gave the following answer [Topology, 9 (1970), 283-298]. Theorem 1 (Murasugi). 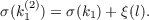 Recall [4] that the invariant ξ(l) is defined by first orienting l, giving, an oriented link l, say, and then setting ξ(l) = σ(l) + Lk(k1,k2), where σ denotes signature and Lk linking number. In the present note we shall give an alternative, more conceptual, proof of Theorem 1, and in fact obtain it as a special case of a considerably more general result. |
Mathematical Subject Classification 2000
Primary: 57M25
|
Milestones
Received: 17 April 1978
Published: 1 May 1979
|
Authors |
| Cameron Gordon | |
| Department of Mathematics The University of Texas at Austin 1 University Station C1200 Austin TX 78712-0257 United States |
|
| http://www.ma.utexas.edu/text/webpages/gordon.html | |
| Richard A. Litherland | |
| Department of Mathematics Louisiana State University Baton Rouge LA 70803 United States |
|
| www.math.lsu.edu/~lither | |
 |
