|

|

|
|
A
converse to (Milnor-Kervaire theorem) ×R etc…
Michael Freedman |
|
Vol. 82 (1979), No. 2, 357–369
|
Abstract |
|
One of the most puzzling questions in low dimensional topology is which elements α ∈ π2(M), where M is a smooth compact 4-manifold, may be represented by a smoothly imbedded 2-sphere. This paper treats a stable version of the problem: When is there a smooth proper imbedding, h : S2 × R↪M × R by which the ends of S2 ×R are mapped to the ends of M × R, and for which the composition 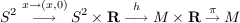 represents α? |
Mathematical Subject Classification 2000
Primary: 57R95
|
Milestones
Received: 1 November 1976
Revised: 16 May 1978
Published: 1 June 1979
|
Authors |
| Michael Freedman | |
| Station Q Microsoft CNSI Bldg. Rm 2245 University of California Santa Barbara CA 93106-6105 United States |
|
| http://stationq.cnsi.ucsb.edu/~freedman/ | |
 |
