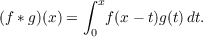|
Let 𝒜 = Lloc1(R+) be the
algebra of locally integrable functions on the positive real axis, with convolution as
multiplication, given by
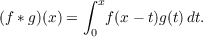
Sometimes it is convenient to think of our functions as being defined on all of R, but
vanishing for negative x. We are interested in subalgebras of 𝒜 that are Banach
algebras in some norm, and that are radical in the sense that there exist no
(nontrivial) complex homomorphisms. We call these algebras radical convolution
algebras. Such algebras A present a challenge because there is no Fourier transform
for them.
We are concerned with the problem of “convolution cut-down”; namely whether
given a radical convolution algebra A and an f ∈ A, there must exist an h ∈ A (h≠0)
such that f ∗h ∈ L1(R+). We show, at least, that one cannot always choose h ∈ L1.
As a corollary, we show that simultaneous convolution cut-down is not always
possible.
|