|
We study the behavior of
the solutions of the second order nonlinear functional differential equation
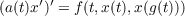 | (1) |
where a, g : [t0,∞) → R and f : [t0,∞) × R2 → R are continuous, a(t) > 0, and
g(t) →∞ as t →∞. We are primarily interested in obtaining conditions which
ensure that certain types of solutions of (1) are nonoscillatory. Conditions which
guarantee that oscillatory solutions of (1) converge to zero as t →∞ are also given.
We apply these results to the equation
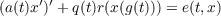 | (2) |
where q : [t0,∞) → R, r : R → R, e : [t0, ∞) × R → R are continuous and a and g
are as above. We compare our results to those obtained by others. Specific examples
are included.
|