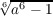An explicit formula for the fundamental units of a real pure sextic number field and its Galois closure

Ken Nakamula

Vol. 83 (1979), No. 2, 463–471

DOI: 10.2140/pjm.1979.83.463

Abstract

The object of this paper is to give a set of fundamental units of a real pure sextic number field K = Q(), where a is a special type of natural number and a⁶ − 1 is not necessarily 6th power free. It is also shown that a set of fundamental units of the galois closure L = K() of K is formed by a real unit and its conjugates.

Mathematical Subject Classification

Primary: 12A40, 12A40

Secondary: 12A45

Milestones

Received: 8 June 1977

Revised: 21 December 1978

Published: 1 August 1979