|

|

|
|
Generalization of a
theorem of Landau
Miriam Hausman |
|
Vol. 84 (1979), No. 1, 91–95
|
Mathematical Subject Classification
Primary: 10A20, 10A20
|
Milestones
Received: 27 January 1977
Revised: 8 March 1979
Published: 1 September 1979
|
Authors |
| Miriam Hausman | |
 |


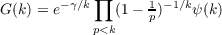
![∏ ∏
ψ(k) = (1− 1)1∕p (1 − 1)(1∕k)[k∕p]+1∕k.
p|k p p∤k p
p<k p<k](a093x.png)
