Translation-invariant operators of weak type

Daniel M. Oberlin

Vol. 85 (1979), No. 1, 155–164

DOI: 10.2140/pjm.1979.85.155

Abstract

Let G be a locally compact group and let m be a left Haar measure on G. For 0 < p < ∞, let L^p(G) be the usual Lebesgue space of functions f on G for which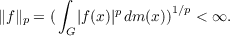

If T is a linear operator which takes L^p(G), or a subspace of L^p(G), into measurable functions on G, then T is said to be of weak type (p,p) if there exists a positive constant C such that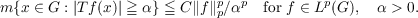

We are interested in the translation-invariant operators of weak type (p,p).

Mathematical Subject Classification 2000

Primary: 43A22

Milestones

Received: 16 October 1978

Published: 1 November 1979