|

|

|
|
Direct limit groups and
the Keesling-Mardešić shape fibration
Kenneth R. Goodearl and Thomas Benny Rushing |
|
Vol. 86 (1980), No. 2, 471–476
|
Abstract |
|
We show that the
Keesling-Mardešić shape fibration has an uncountable number of fibers of different
shape type. This is done by showing that an uncountable number of nonisomorphic
groups can arise as direct limits of direct limit sequences having all groups Z⊕Z and
all bonding homomorphisms given by one of the two matrices |
Mathematical Subject Classification 2000
Primary: 55R65
Secondary: 55P55
|
Milestones
Received: 30 March 1979
Published: 1 February 1980
|
Authors |
| Kenneth R. Goodearl | |
| University of California, Santa
Barbara Santa Barbara CA United States |
|
| Thomas Benny Rushing | |
 |
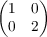 or
or
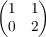 .
.