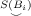A decomposition of complete Boolean algebras

Spiros Argyros

Vol. 87 (1980), No. 1, 1–9

DOI: 10.2140/pjm.1980.87.1

Abstract

Denoting by |B| the cardinality of a Boolean algebra B and by S(B) the least cardinal κ such that every family of mutually disjoint elements of B has cardinality less than κ, we prove that: if B is a complete Boolean algebras, then there is a finite family B₁,⋯,B_n of complete Boolean algebra, such that B is isomorphic to the product B₁ ×⋯ × B_n, and |B_i| = |B_i| for i = 1,2,⋯,n.

Mathematical Subject Classification 2000

Primary: 06E10

Secondary: 03G05

Milestones

Received: 6 April 1979

Revised: 16 May 1979

Published: 1 March 1980