Inner functions: noninvariant connected components

Vassili Nestoridis

Vol. 87 (1980), No. 1, 199–209

DOI: 10.2140/pjm.1980.87.199

Abstract

H denotes the family of all inner functions B, such that for every 𝜃 ∈ ]0,1[ the pseudo-hyperbolic diameters of the connected components of the set ∑ _B,𝜃 = {z : |B(z)| < 𝜃} are less than δ_B,𝜃 < 1.

Family H is open-closed in the space of the inner functions under the uniform topology. The main result states that for every B ∈ H the connected component of B contains neither proper multiples of B nor proper divisors of B. A characterization of the elements of H is given, which in particular implies that if the zeros α_n, n = 1,2,⋯ of an infinite Blaschke product B satisfy condition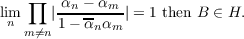

Mathematical Subject Classification 2000

Primary: 30D50

Milestones

Received: 21 November 1978

Revised: 21 June 1979

Published: 1 March 1980