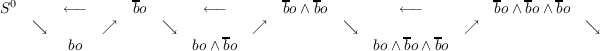|
The real connective
K-theory spectrum, bo, has been shown to be a useful spectrum in homotopy theory.
In particular, the bo-homology Adams Spectral Sequence, based on the cofiber
sequence
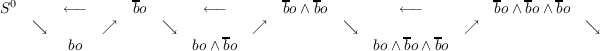 | (A) |
has been used extensively by Mahowald in his work on the image of the
J-homomorphism. One of the problems encountered with the bo-spectrum is that,
unlike the mod 2 Eilenberg-Maclane spectrum, bo∧bo does not split as a wedge of
suspensions of bo itself. However, Mahowald and Milgram have obtained a
splitting
 | (B) |
where X is a wedge of spaces intimately related with bo itself, and G is a wedge of
mod 2 Eilenberg-MacLane spectra. In this paper, we determine the structure of G,
i.e., we calculate the number of Eilenberg-Maclane summands occuring in each
dimension.
|