Naturally integrable functions

Lester Eli Dubins and David Samuel McIntyre Margolies

Vol. 87 (1980), No. 2, 299–312

DOI: 10.2140/pjm.1980.87.299

Abstract

A bounded function f defined on an amenable group G is naturally integrable if, for every pair of left-invariant means μ and μ′, μ(f) = μ′(f). If G is the additive group of integers, then (i) f is naturally integrable if, and only if,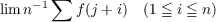

exists uniformly in j , and (ii) the associated natural measure ν is convex; that is, for every pair of naturally measurable sets of integers E₀ and E₁ with E₀ ⊂ E₁, there is a monotone family of naturally measurable sets E_t (0 ≦ t ≦ 1) such that ν(E_t) (0 ≦ t ≦ 1) is a closed interval. Analogous results hold for the presently known amenable groups.

Mathematical Subject Classification 2000

Primary: 43A07

Milestones

Received: 21 December 1978

Published: 1 April 1980