On curvature operators of bounded rank

Jaak Vilms

Vol. 87 (1980), No. 2, 467–473

DOI: 10.2140/pjm.1980.87.467

Abstract

A curvature operator, that is, a linear map R : Λ²V → Λ²V , has bounded rank 2r if it maps simple bivectors into bivectors of rank ≦ 2r. It is shown here that this condition is equivalent to the following: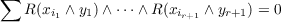

for all x₁,⋯,x_r+1, y₁,⋯,y_r+1 in V , with the sum taken over all permutations (i₁,⋯,i_r+1) of (1,2,3,⋯,r + 1). An application to Riemannian geometry is given.

Mathematical Subject Classification 2000

Primary: 53B20

Milestones

Received: 17 November 1978

Revised: 10 July 1979

Published: 1 April 1980