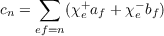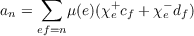A double inversion formula

John David Brillhart

Vol. 89 (1980), No. 1, 7

DOI: 10.2140/pjm.1980.89.7

Abstract

Let G be an abelian group and suppose {a_n} and {b_n}, n ≧ 1, are sequences in G. Let p be an odd prime and set η_e = (e₁∕p), the Legendre symbol, where e = p^se₁, s ≧ 0, p|̸e₁. Also, let χ_e^± = (1 ± η_e)∕2. Define the sequence {c_n} and {d_n}, n ≧ 1, by

(1)

and

(2)

Theorem. For n ≧ 1 and μ the Möbius function,

(3)

and

(4)

Mathematical Subject Classification

Primary: 10A20, 10A20

Milestones

Received: 8 June 1979

Published: 1 July 1980