Maps on simple algebras preserving zero products. I. The associative case

Warren James Wong

Vol. 89 (1980), No. 1, 229–247

DOI: 10.2140/pjm.1980.89.229

Abstract

Recent studies of linear transformations of various types on the space of n × n matrices over a field suggest the general problem of finding the semilinear transformations f on an algebra A over a field k, with the property that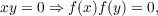

where x,y ∈ A. In this article such maps are determined for a class of primitive associative algebras, including the case of bijective maps f on a finite-dimensional simple associative algebra A.

Mathematical Subject Classification 2000

Primary: 15A04

Secondary: 16A20

Milestones

Received: 31 May 1978

Published: 1 July 1980