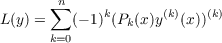Comparison and oscillation criteria for selfadjoint vector-matrix differential equations

Roger T. Lewis and Lynne C. Wright

Vol. 90 (1980), No. 1, 125–134

DOI: 10.2140/pjm.1980.90.125

Abstract

Let

where the coefficients are real, continuous, m × m, symmetric matrices, y(x) is an m-dimensional vector-valued function, and P_n(x) is positive definite for all x ∈ I. We consider both the case for which the singularity is at ∞, I = [1,∞), and the case for which the singularity is at 0, I = (0,1].

The main theorem is a comparison result in which the equation L(y) = 0 is compared with an associated scalar equation. Then, general theorems for the oscillation and nonoscillation of L(y) = 0 are presented which can be used when the comparison theorem does not apply. Some of the proofs indicate how scalar oscillation and nonoscillation criteria can be extended to the vector-matrix case when the associated scalar theorem has been proved using the quadratic functional criteria for oscillation. In general, proofs using the associated Riccati equation and other familiar methods do not extend as easily.

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 3 January 1979

Revised: 29 November 1979

Published: 1 September 1980