A note on the Konhauser sets of biorthogonal polynomials suggested by the Laguerre polynomials

H. M. (Hari Mohan) Srivastava

Vol. 90 (1980), No. 1, 197–200

DOI: 10.2140/pjm.1980.90.197

Abstract

Two new classes of bilateral generating functions are given for the Konhauser polynomials Y _n^α(x;k), which are biorthogonal to the Konhauser polynomials Z_n^α(x;k) with respect to the weight function x^αe^−x over the interval (0,∞), α > −1 and k = 1,2,3,⋯ . The bilateral generating functions (1) and (2) below would reduce, when k = 1, to similar results for the generalized Laguerre polynomials L_n^(α)(x). Furthermore, for k = 2, these formulas yield the corresponding properties of the Preiser polynomials.

It is also shown how the bilateral generating function (2) can be applied to derive a new generating function for the product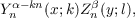

where α,β > −1, k,l = 1,2,3,⋯ , and n = 0,1,2,⋯ .

Mathematical Subject Classification

Primary: 33A65, 33A65

Milestones

Received: 2 November 1979

Published: 1 September 1980