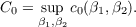The best two-dimensional Diophantine approximation constant for cubic irrationals

William Wells Adams

Vol. 91 (1980), No. 1, 29–30

DOI: 10.2140/pjm.1980.91.29

Abstract

Let 1, β₁, β₂ be a basis of a real cubic number field K. Let c₀ = c₀(β₁β₂) be the infimum over all constants c > 0 such that

has an infinite number of solutions in integers q > 0, p₁, p₂. Set

The purpose of this note is to observe that combining a recent beautiful result in the geometry of numbers of A. C. Woods with the earlier work of the author, we obtain

Theorem. C_O = 2∕7.

Mathematical Subject Classification

Primary: 10E15, 10E15

Secondary: 10F10

Milestones

Received: 25 June 1980

Published: 1 November 1980