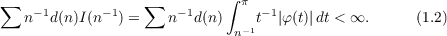|C, 1| summability of series associated with Fourier series

The purpose of this paper is to prove the following theorem. Suppose that for u ≥ n₀, g(u) and d(u) are positive functions such that ud(u) is nondecreasing and (i) ∑ n⁻¹g(n)d(n) < ∞. Then the series ∑ d(n)A_n(x) is summable |C,1|, if the following hold:

∫ t −1 Φ(t) = 0 |φ(u)|du = O (tg(t )), t −→ +0; (1.1)

∑ ∑ ∫ π n−1d(n )I(n−1) = n−1d(n) t−1|φ(t)|dt < ∞. (1.2) n−1

Mathematical Subject Classification

Primary: 42A28

Milestones

Received: 5 June 1979

Revised: 18 September 1979

Published: 1 December 1980

Authors

H. P. Dikshit


S. N. Dubey

Vol. 91, No. 2, 1980

H. P. Dikshit and S. N. Dubey

Abstract

Mathematical Subject Classification

Milestones

Authors