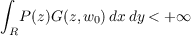The equations Δu = Pu (P ≧ 0) on Riemann surfaces and isomorphisms between relative Hardy spaces

Takeyoshi Satō

Vol. 92 (1981), No. 1, 173–194

DOI: 10.2140/pjm.1981.92.173

Abstract

It has been demonstrated by M. Nakai that the Banach spaces PB (the space of bounded solutions on R of the equation Δu = Pu, P ≥ 0) and HB (the space of bounded harmonic functions on R) are isometrically isomorphic whenever the condition

is valid for some point w₀ in R (z = x + iy). Here, G(z,w) is the harmonic Green’s function on R. In this paper we shall show, under the preceding condition that the Hardy space H^p, 1 < p ≤ +∞, of harmonic functions on a hyperbolic Riemann surface R is isometrically isomorphic to the relative Hardy space PH_w^p of quotients of solutions of Δu = Pu by the P-elliptic measure w of R.

Mathematical Subject Classification 2000

Primary: 30F15

Secondary: 30F20, 31A35

Milestones

Received: 3 January 1979

Published: 1 January 1981