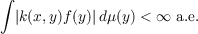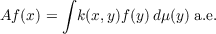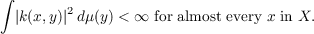Unitary equivalence to integral operators

Viakalathur Shankar Sunder

Vol. 92 (1981), No. 1, 211–215

DOI: 10.2140/pjm.1981.92.211

Abstract

A bounded operator A on L²(X) is called an integral operator if there exists a measurable function k on X ×X such that, for each f in L²(X),

and

(Throughout this paper, (X,μ) will denote a separable, σ-finite measure space which is not purely atomic.) An integral operator is called a Carleman operator if the inducing kernel k satisfies the stronger requirement:

Mathematical Subject Classification 2000

Primary: 47B38

Secondary: 47G05

Milestones

Received: 5 January 1978

Published: 1 January 1981