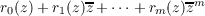Approximation by rational modules on boundary sets

James Li-Ming Wang

Vol. 92 (1981), No. 1, 237–239

DOI: 10.2140/pjm.1981.92.237

Abstract

Let X be a compact subset of the complex plane. Let the module ℛ(X)𝒫_m be the space of all functions of the form

where each r_i is a rational function with poles off X. We prove that ℛ(X)𝒫₁ is dense in L^p(∂X) for all 1 ≦ p < ∞.

Mathematical Subject Classification 2000

Primary: 30E10

Milestones

Received: 13 February 1979

Revised: 15 February 1980

Published: 1 January 1981