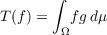Representation of compact and weakly compact operators on the space of Bochner integrable functions

Kevin T. Andrews

Vol. 92 (1981), No. 2, 257–267

DOI: 10.2140/pjm.1981.92.257

Abstract

If X^∗ has the Radon-Nikodym property, then for every compact operator T : L₁(μ,X) → Y there is a bounded function g : Ω → L(X,Y ) that is measurable for the uniform operator topology on L(X,Y ) such that

for all f in L₁(μ,X). The same result holds for weakly compact operators if X^∗ is separable Schur space. These representations yield Radon-Nikodym theorems for operator valued measures and a generalization of a theorem of D. R. Lewis.

Mathematical Subject Classification 2000

Primary: 47B38

Secondary: 46E40, 47B05

Milestones

Received: 24 September 1979

Revised: 15 February 1980

Published: 1 February 1981