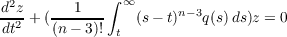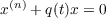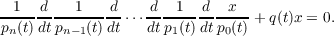Oscillation criteria for general linear ordinary differential equations

Takaŝi Kusano and Manabu Naito

Vol. 92 (1981), No. 2, 345–355

DOI: 10.2140/pjm.1981.92.345

Abstract

Lovelady has recently proved the following oscillation theorem.

Theorem. Let n ≧ 4 be even and q : [a,∞) → (0,∞) be continuous. If ∫ ^∞tⁿ⁻²q(t)dt < ∞ and the second order equation

is oscillatory, then the n-th order equation

is oscillatory.

In this paper the above theorem will be extended to a class of differential equations of the form

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 3 October 1979

Published: 1 February 1981