|
If β is an algebraic number of
degree n + 1 then the number of solutions α, with α algebraic of degree at most n, to
the inequalities
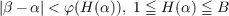 | (1) |
is studied using methods developed by Schmidt and Adams for counting solutions to
inequalities involving linear forms. In (1) H(α) is a height function which
differes slightly from the usual height and φ is a function which decreases to
zero.
If φ(y)yn+1 →∞ as y →∞ then the number of solutions is given as
an integral plus an error term. If φ(y)yn+1 is constant then the number
of solutions is either bounded or asymptotic to C log B for some constant
C.
|