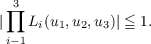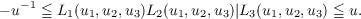The asymmetric product of three homogeneous linear forms

Alan C. Woods

Vol. 93 (1981), No. 1, 237–250

DOI: 10.2140/pjm.1981.93.237

Abstract

Let L_i = ∑ _j=1³a_ijx_j, i = 1,2,3, be three linear forms in the variables x₁, x₂, x₃ with real coefficients a_ij. A theorem of Davenport asserts that, if |det(a_ij)| = 7, then there exist integers u₁, u₂, u₃, not all zero, such that

Under the same hypothesis, W. H. Adams has asked whether, given a positive real number u, there exist integers u₁, u₂, u₃, not all zero, such that

Our objective is to prove this conjecture.

Mathematical Subject Classification

Primary: 10E15, 10E15

Secondary: 10E20, 10C25

Milestones

Received: 30 August 1979

Revised: 7 March 1980

Published: 1 March 1981