|

|

|
|
On the topology of
direct limits of ANRs
Richard Elam Heisey and Henryk Torunczyk |
|
Vol. 93 (1981), No. 2, 307–312
|
Abstract |
||||||||
|
Let {(Xn,an)} be a sequence of pointed, locally compact, finite-dimensional, nondegenerate, connected ANR’s. It is shown that the direct limit of the system
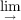 Rn, R the reals. As a consequence, if
f : X → Y is a homotopy equivalence between ANR’s as above then Rn, R the reals. As a consequence, if
f : X → Y is a homotopy equivalence between ANR’s as above then
 fn : fn : 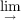 Xn → Xn →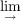 Y n is homotopic to a homeomorphism. Y n is homotopic to a homeomorphism.
|
Mathematical Subject Classification 2000
Primary: 57N20
Secondary: 54C55, 58B20
|
Milestones
Received: 15 June 1979
Revised: 7 February 1980
Published: 1 April 1981
|
Authors |
| Richard Elam Heisey | |
| Henryk Torunczyk | |
 |
