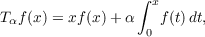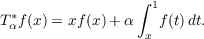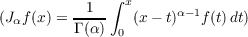Invariant subspace lattices for a class of operators

Boon-Hua Ong

Vol. 94 (1981), No. 2, 385–405

DOI: 10.2140/pjm.1981.94.385

Abstract

We study the invariant subspace lattices for a one parameter family of operators {T_α}_α on L^p(0,1), α a complex number, where

and their adjoints T_α^∗,

The closed invariant subspaces for T_α are in one-to-one correspondence with certain closed ideals of ℛ_α, where ℛ_α is a Silov algebra with unit and in which the range ℛ_α of the Riemann Liouville operator J_α

is embedded as a closed ideal. When n is a positive integer, there is a complete lattice isomorphism between the closed ideals of ℛ_n and the n-tuples (E₀,E₁,⋯,E_n−1) of closed subsets of [0,1] where E₀ ⊇ E₁ ⊇⋯ ⊇ E_n−1 ⊇ derived set of E₀. Every closed ideal of ℛ_n is the intersection of closed primary ideals. Similar results carry over to α where the real part of α is an integer and also to the adjoint operators.

Mathematical Subject Classification 2000

Primary: 47A15

Secondary: 46J10

Milestones

Received: 9 August 1980

Published: 1 June 1981