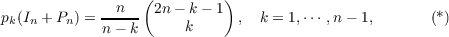Monotonicity of permanents of certain doubly stochastic matrices

David London

Vol. 95 (1981), No. 1, 125–131

DOI: 10.2140/pjm.1981.95.125

Abstract

Let p_k(A), k = 1,⋯,n, denote the sum of the permanents of all k × k submatrices of the n × n matrix A.

We prove that

where I_n and P_n are respectively the n × n identity matrix and the n × n permutation matrix with 1’s in positions (1,2),(2,3),⋯,(n − 1,n),(n,1). Using (∗), we prove that for n ≧ 3 and A = (I_n + P_n)∕2, the functions

are strictly monotonic increasing in the interval 0 ≦ 𝜃 ≦ 1. Here J_n is the n × n matrix all whose entries are equal to 1∕n.

Mathematical Subject Classification 2000

Primary: 15A15

Secondary: 15A51

Milestones

Received: 9 January 1980

Published: 1 July 1981