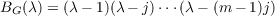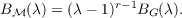The fixed-point partition lattices

Philip Hanlon

Vol. 96 (1981), No. 2, 319–341

DOI: 10.2140/pjm.1981.96.319

Abstract

Let σ be a permutation of the set {1,2,⋯,n} and let Π(N) denote the lattice of partitions of {1,2,⋯,n}. There is an obvious induced action of σ on Π(N); let Π(N)_σ = L denote the lattice of partitions fixed by σ.

The structure of L is analyzed with particular attention paid to ℳ, the meet sublattice of L consisting of 1 together with all elements of L which are meets of coatoms of L. It is shown that ℳ is supersolvable, and that there exists a pregeometry on the set of atoms of ℳ whose lattice of flats G is a meet sublattice of ℳ. It is shown that G is supersolvable and results of Stanley are used to show that the Birkhoff polynomials B_ℳ(λ) and B_G(λ) are

and

Here m is the number of cycles of σ, j is square-free part of the greatest common divisor of the lengths of σ and r is the number of prime divisors of j. ℳ coincides with G exactly when j is prime.

Mathematical Subject Classification 2000

Primary: 06C10

Secondary: 05B35

Milestones

Received: 16 July 1980

Published: 1 October 1981